Neural Cellular Automata (NCAs) are bio-inspired systems in which identical cells self-organize to form complex and coherent patterns by repeatedly applying simple local rules. NCAs display striking emergent behaviors including self-regeneration, generalization and robustness to unseen situations, and spontaneous motion. Despite their success in texture synthesis and morphogenesis, NCAs remain largely confined to low-resolution grids (typically 128 $\times$ 128 or smaller). This limitation stems from (1) training time and memory requirements that grow quadratically with grid size, (2) the strictly local propagation of information which impedes long-range cell communication, and (3) the heavy compute demands of real-time inference at high resolution. In this work, we overcome this limitation by pairing NCA with a tiny, shared implicit decoder, inspired by recent advances in implicit neural representations. Following NCA evolution on a coarse grid, a lightweight decoder renders output images at arbitrary resolution. We also propose novel loss functions for both morphogenesis and texture‐synthesis tasks, specifically tailored for high‐resolution output with minimal memory and computation overhead. Combining our proposed architecture and loss functions brings substantial improvement in quality, efficiency, and performance. NCAs equipped with our implicit decoder can generate full-HD outputs in real time while preserving their self-organizing, emergent properties. Moreover, because each MLP processes cell states independently, inference remains highly parallelizable and efficient. We demonstrate the applicability of our approach across multiple NCA variants (on 2D, 3D grids, and 3D meshes) and multiple tasks, including texture generation and morphogenesis (growing patterns from a seed), showing that with our proposed framework, NCAs seamlessly scale to high-resolution outputs with minimal computational overhead.
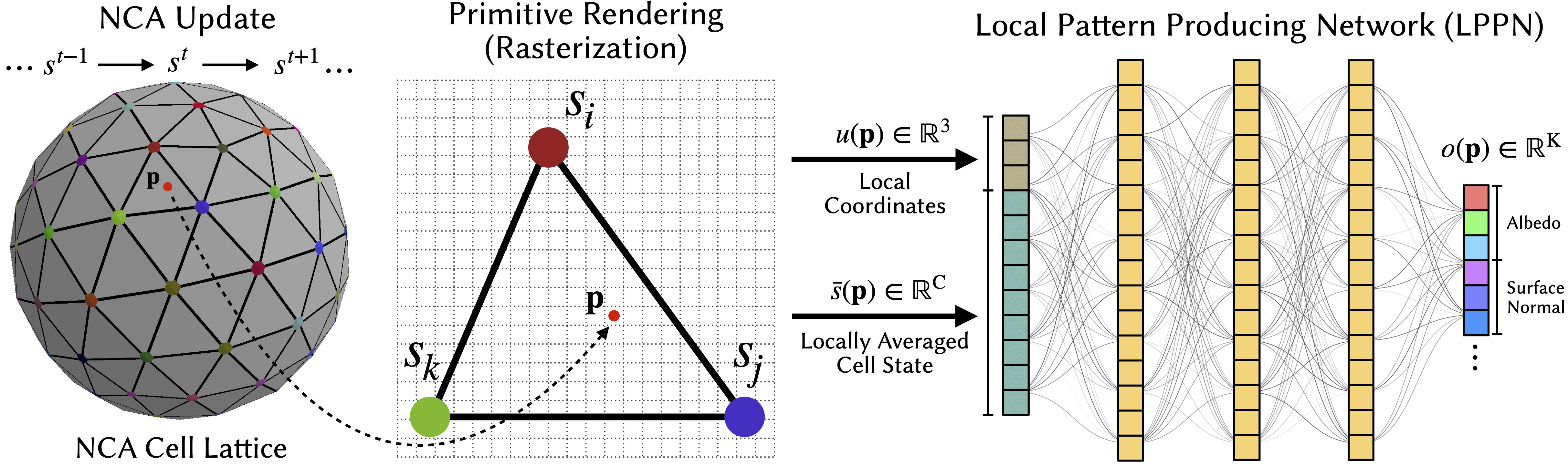
The NCA operates on a coarse lattice of cells (in this example vertices of a mesh). Center: A sampling point \(\Point\) (red dot) inside a triangle primitive, whose vertices correspond to NCA cells \(\State_i,\,\State_j,\,\State_k\). The local coordinate \(u(\Point)\) expresses the point’s position inside the primitive, while the locally averaged cell state \(\bar{\State}(\Point)\) is obtained by interpolating the surrounding cell states. Right: The Local Pattern Producing Network (LPPN), A shared lightweight MLP, receives \((\bar{\State}(\Point), u(\Point))\) as input and outputs the target properties, such as color and surface normal, at point \(\Point\). The NCA and the LPPN are trained jointly and end-to-end.
Play with the interactive visualization below to see coarse NCA cell states and the output the LPPN generates.
Ehsan
Yitao
Ali
Alex
Wenzel
Sabine
@misc{cells2pixels,
title = {Neural Cellular Automata: From Cells to Pixels},
author = {Pajouheshgar, Ehsan and Xu, Yitao and Abbasi, Ali and Mordvintsev, Alex and Jakob, Wenzel and S{\"u}sstrunk, Sabine},
year = {2025}
note = {arXiv preprint}
}